





Published on Feb 13, 2025
The objective: This project aims to dispel a common belief that a single piece of paper can be folded in half no more than seven times. We conducted experiments to determine what factors affected the number of times a paper can be folded, and we created a program to simulate paper folding based on our observations. Our discoveries can help manufacturing industries know how to fold and package their products to minimize space.
The purpose of this experiment is to test the belief that a sheet of paper can only be folded seven times, and determine the effect of the size and thickness of the paper.
A sheet of paper can be folded in half no more than seven times, according to popular belief.
Dimensions of paper – Independent variable
Thickness of paper – Independent variable
Number of folds the paper can have – Dependent variable
In this experiment, we will control for one independent variable to see the effects that the other independent variable has on the number of folds. In other words, we will use paper of the same thickness, but different dimensions, and also paper of the same dimensions but different thicknesses.
2 sheets, standard printing paper:
(215.9 x 279.4 mm) and (107.95 x 139.7 mm)

1. A sheet of standard printing paper (dimensions: 215.9 x 279.4 mm, thickness: 0.1mm) was folded in half about its longest side.
2. Step 1 was repeated until the paper can no longer be folded.
3. Steps 1 and 2 were repeated with a new sheet of paper three times.
4. The average of number of times that the three papers were folded was rounded and recorded.
1. Part A was repeated with a smaller sheet of paper (dimensions: 107.95 x 139.7 mm, thickness: 0.1mm).
1. Part A was repeated with a thicker sheet of paper (dimensions: 215.9 x 279.4 mm, thickness: 0.4mm).
1. Part A was repeated with a thicker and smaller sheet of paper (dimensions: 107.95 x 139.7 mm, thickness: 0.4mm).
1. Part A was repeated with a thinner sheet of paper (dimensions: 215.9 x 279.4 mm, thickness: 0.05mm).
1. Part A was repeated with a thinner and smaller sheet of paper (dimensions: 107.95 x 139.7 mm, thickness: 0.05mm).
1. Part A was repeated with a thinner and larger sheet of paper (dimensions: 5080 x 7620mm, thickness: 0.05mm).
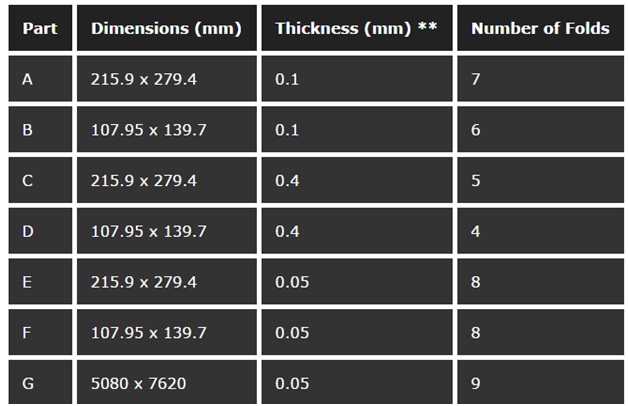
In conclusion, the hypothesis that a sheet of paper can only fold maximum seven times is incorrect. It is possible to fold a sheet of paper more than seven times if it is thin enough and/or large enough. For most of the data from this experiment, the number of times a sheet of paper can fold is proportional to the dimensions and the thickness. For example, when the length and width of a paper is halved, the number of times it can fold decreases by one. Also, when the thickness is doubled, the number of folds decreases by one.
In other words:
The relation between thickness and number of folds is, n = floor( -log2t )
The relation between the length of the longest side and number of folds is, n = floor( log2w )
n is the number of folds more than the control, t is the ratio of the thickness compared to the thickness of the control, w is the ratio of the side length compared to the side length of the control.
For example, if t is two times the size of T (thickness of the control), and the control can fold seven times:
n = floor( -log2t )
n = floor( -log22 )
n = -1
Therefore, the sheet can fold 1 time less than the control, i.e. 6 times in total. We can expand on these relations to write an equation to model paper folding mathematically without comparing it to a control.
Not all of the results in this experiment followed the relations. The results that did not follow the relations are Part F and Part G. According to the relation between side length and number of folds, Part F should fold 7 times, since the dimensions are halved compared to Part E. In addition, since the side length of Part G is 27 times larger than Part E, it should fold n = 4 times more than Part E, so 12 times in total. These anomalies may be caused by the sources of error.
Some ways to expand on this experiment, other than to eliminate the sources of error, are to test for the number of folds for paper of different shapes, and to determine if folding lengthwise or widthwise affects the number of times it can fold. To elaborate, we can compare the number of folds of a square sheet of paper to a long, narrow sheet of the same area to see if the shape affects the number of folds. We can also try different ways to fold the paper and find the way to get the maximum number of folds. Instead of folding the longest side each time, we can see if the method: folding it about one side until it could no longer be folded, then folding it about the other side, will result in a different number of folds.
Conley, Ken. "Episode 72: Underwater Car and Seven Folds." Annotated Mythbusters. Ken Conley, 24 Jan. 2007. Web. 15 Apr. 2014. <http://kwc.org/mythbusters/2007/01/episode_72_underwater_car_and.html>.
Historical Society of Pomona Society. "Folding Paper in Half Twelve Times."Folding Paper in Half Twelve Times. Historical Society of Pomona Society, n.d. Web. 12 Apr. 2014. <http://pomonahistorical.org/12times.htm>.
Stier, Caitlin. "Students Break Record by Folding Toilet Paper 13 times." New Scientist TV. New Scientist, 11 Jan. 2012. Web. 12 Apr. 2014. <http://www.newscientist.com/blogs/nstv/2012/01/paper-folding-limits-pushed.html>.
Weisstein, Eric W. "Folding." From MathWorld-A Wolfram Web Resource, n.d. Web. 18 Apr.2014 <http://mathworld.wolfram.com/Folding.html>